Mutexes in Graphplan

Graphplan: mutexes and example

There are two types of binary mutual exclusion relations (called mutex) in Graphplan.

mutexes between pairs of actions. They are marked between actions at the action levels (S0, S1, etc). The actions in the pair can be maintenance actions (or, as they are called in the texbook, persistence actions) or other actions, since from the point of view of being in a mutex the type of action does not make any difference. the

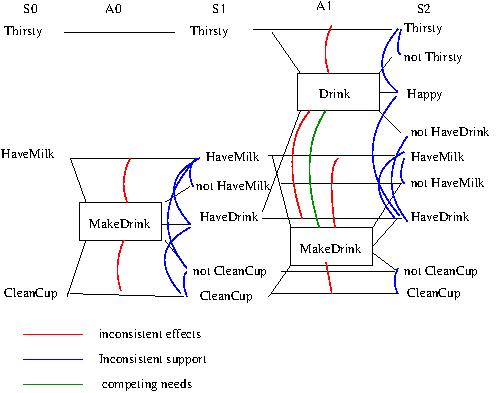
Inconsistent Effects: the effect of one action is the negation of another action's effect.
At least one of the two actions has to be a non-persistence action. Opposite persistence actions have inconsistent effects (trivially) and are marked at the proposition level as having inconsistent support.

The curved line in the figure indicates an inconsistent effect between the two actions, since the effect of one is the negation of the effect of the other.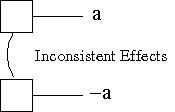

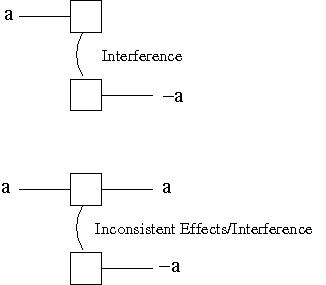
Interference: one action deletes a precondition of another.
This is between two actions that are not persistence actions.

The curved line in the figure indicates an interference between the two actions, since the effect of one is the negation of the effect of the other.

The second figure shows that inconsistent effects can also produce interference. When one of the actions is a persistence action we do not mark Interference since the mutex is already marked as Inconsistent Effects.

Competing Needs: the actions have preconditions that are mutex.
This is used only for actions that are not persistence actions, since opposite persistence actions have competing needs trivially.

The curved line in the figure indicates Competing Needs between the two actions, since their preconditions are in mutex.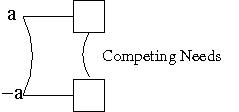

mutexes between pairs of propositions. They are marked at the proposition levels (S0, S1, etc).

a proposition and its negation are mutex

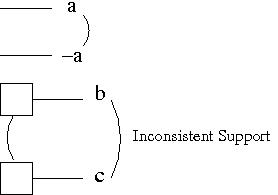
Inconsistent Support: all the ways of achieving the propositions are pairwise mutex.

The curved line in the top figure indicates a mutex between two propositions since one is the negation of the other.

In the second figure, there is Inconsistent Support since the only way of achieving the two propositions is mutex. This figure assumes there are no other ways of achieving the two propositions.

Extraction of a solution

To know if a solution has been reached the first step is to see if the propositions in the goal are all present at the current level and none are pairwise mutex. If not the planning graph needs to be expanded by adding another action and another proposition level. The existence of all the goal propositions at the current level is a necessary but not sufficient condition for having a solution.
The next step is to try to extract a solution. Here is where the mutexes are used to see if there is a consistent (i.e. with no mutexes) way of achieving all the subgoals. This is done as a search process that starts at the current level and searches backwards subgoal by subgoal and level by level. If the search fails after having tried all the ways of achieving each subgoal in every possible way, Graphplan extends the planning graph and tries again.

Graphplan example

Given the following STRIPS action schemas, initial state, and goal:

Action:MakeDrink,
Precond: CleanCup ∧ HaveMilk
Effect: HaveDrink ∧ ¬ CleanCup ∧ ¬ HaveMilk

Action:Drink,
Precond: Thirsty ∧ HaveDrink
Effect: Happy ∧ ¬ Thirsty ∧ ¬ HaveDrink

Initial State: Thirsty ∧ CleanCup ∧ HaveMilk

Goal: Happy

drink example

The goal is reached at level S2 with the action Drink. The action Drink can be done after the action MakeDrink, which can be done in the initial state S0.