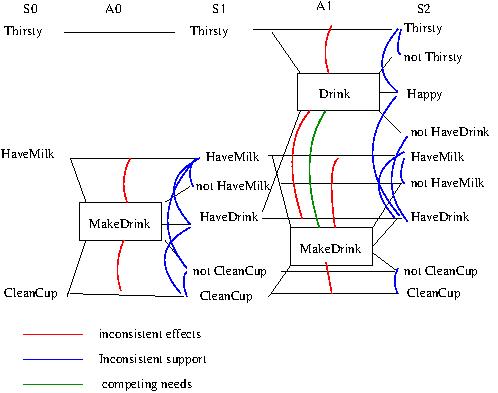
- Inconsistent Effects: the effect of one
action is the negation of another action's effect.
At least one of the two actions has to be a non-persistence action. Opposite persistence actions have inconsistent effects (trivially) and are marked at the proposition level as having inconsistent support.The curved line in the figure indicates an inconsistent effect between the two actions, since the effect of one is the negation of the effect of the other. 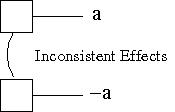
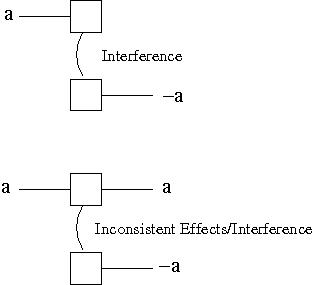
- Interference: one action deletes a
precondition of another.
This is between two actions that are not persistence actions.The curved line in the figure indicates an interference between the two actions, since the effect of one is the negation of the effect of the other. The second figure shows that inconsistent effects can also produce interference. When one of the actions is a persistence action we do not mark Interference since the mutex is already marked as Inconsistent Effects.
- Competing Needs: the actions have
preconditions that are mutex.
This is used only for actions that are not persistence actions, since opposite persistence actions have competing needs trivially.The curved line in the figure indicates Competing Needs between the two actions, since their preconditions are in mutex. 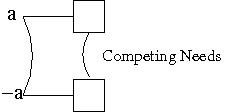
- a proposition and its negation are mutex
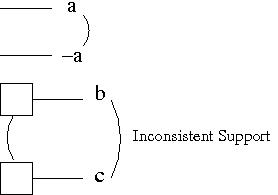
- Inconsistent Support: all the ways of
achieving the propositions are pairwise mutex.
The curved line in the top figure indicates a mutex between two propositions since one is the negation of the other. In the second figure, there is Inconsistent Support since the only way of achieving the two propositions is mutex. This figure assumes there are no other ways of achieving the two propositions.